|
Click to enlarge
|
|
The inception of the third millennium can boast an extended pedigree as a symbol for new beginnings. In a work written in 1884, the hero of science fiction’s most celebrated tale about expanding horizons contemplates his limited world at this crucial moment:
It was the last day of the 1999th year of our era… and I was … musing on the events of the past and the prospects of the coming year, the coming century, the coming Millennium… There I sat by my wife’s side, endeavoring to form a retrospect of the year 1999 and of the possibilities of the year 2000.
And as A Square took stock of his life in the two-dimensional universe of E.A. Abbott’s Flatland, a sphere from an incomprehensible world of higher dimensionality passed right through the plane of his entire existence, appearing first as a point, and then as a circle of initially expanding and subsequently diminishing radius — while A Square looked on in stunned awe and utter mystification. The sphere spoke to A Square: “I am indeed, in a certain sense a Circle, and a more perfect Circle than any in Flatland; but to speak more accurately, I am many Circles in one.” A Square then looked at his timepiece, and noted the maximally auspicious moment of the sphere’s passage: “The last sands had fallen. The third Millennium had begun.”
|
Click to enlarge
|
 |
As a technique for the most concrete form of mind-stretching, the study of optical illusions surely matches the contemplation of dimensions beyond our sensory experience (or even our mental conceivability). Many classical illusions present alternatives in two dimensions — as in the duck-rabbit (Figure 1) or urn-faces of gestalt switching between figure and ground. T.S. Kuhn invoked this famous illusion as a primary metaphor to illustrate his central concept of paradigm shifting in The Structure of Scientific Revolutions (1962): “It is as elementary prototypes for these transformations of the scientist’s world that the familiar demonstrations of a switch in visual gestalt prove so suggestive. What were ducks in the scientist’s world before the revolution are rabbits afterwards.” Other illusions present alternatives in three dimensions — as in the famous Necker Cube, so effectively used by Richard Dawkins (in The Extended Phenotype, 1982) to argue for the compatibility of gene-centered and organism-centered views of natural selection. Dawkins writes:
|
Click to enlarge
|
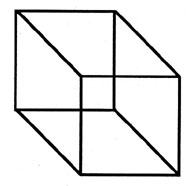 |
There is a well-known visual illusion called the Necker Cube (Figure 2). It consists of a line drawing which the brain interprets as a three-dimensional cube. But there are two possible orientations of the perceived cube, and both are equally compatible with the two-dimensional image on the paper. We usually begin by seeing one of the two orientations … After a few seconds the mental image flips back and it continues to alternate as long as we look at the picture. The point is that neither of the two perceptions of the cube is the correct or ‘true’ one. They are equally correct.
If these familiar illusions in our palpable worlds of two and three dimensions have furnished such useful images for contemplating the nature of major innovations in scientific thinking, consider what we might gain if we could join the two methodologies and create a representation for alternative states in a four dimensional world that we cannot draw and scarcely know how to conceive.
In fact, a stunning example of such a double whammy in mental extension (an optical illusion based on alternative states in four dimensional perspective) was constructed more than eighty years ago by one of the greatest artists of our century: Marcel Duchamp (1887-1968). He published the illusion in 1967 — as a puzzle on a piece of stiffened paper, resembling a postcard in size and shape, and containing an original painting on one side and a verbal explanation on the other. Nevertheless, his evident intention and brilliant realization have never been deciphered.
Many reasons for past failure may be cited. Some can be laid firmly at Duchamp’s door as the desired consequence of his own cryptic intentions. As the enfant terrible of Dada (in the usual interpretation of art historians) — the man who “embellished” a reproduction of the Mona Lisa with a beard and moustache and called the result “art”; the man who signed an ordinary urinal and placed the object on display as his own sculpture, entitled “Fountain,” at a famous art show — Duchamp never deigned to explain his artistic theories or intentions.
But equal or greater weight must be placed upon our own failure to ask the right questions, largely because we have operated under a false taxonomy of intellectual disciplines — one that drives a powerful but illusory wedge of maximal separation between art (viewed as an ineffably “creative” activity, based on personal idiosyncrasy and subject only to hermeneutical interpretation), and science (viewed as a universal and rational enterprise, based on factual affirmation and analytical coherence).
Duchamp ranks as an artist in this false dichotomy — and as a maddeningly cryptic member of his calling to boot. Thus, we have never asked the right questions because we have not recognized the serious and well informed treatment of scientific issues, ranging from optics to the mathematics of probability and dimensionality, pervading so much of Duchamp’s art — and illustrating, in a manner unmatched since Leonardo himself, the fundamental compatibility between these two great domains of human creativity. Many scholars have recognized and documented the numerous scientific allusions throughout Duchamp’s oeuvre, but have then assumed that Duchamp could never be regarded as an innovator of scientific concepts, if only because artists, in our stereotypical view, cannot develop sufficient expertise to understand such technical subjects. Duchamp’s playful or sarcastic allusions to science must therefore represent a grand sardonic joke, an extended reflection by a creative spirit upon the sterility of technological precision.
But several of the great iconoclasts who founded various movements in modern art at the beginning of the 20th century showed serious concern for contemporary science, particularly for concepts of non-Euclidean geometry and the fourth dimension — although they did not employ these ideas in more than a metaphorical, albeit enlightening, way. Duchamp, however, through a combination of general brilliance and rigorous education in the best traditions of French Cartesian schooling, developed a far deeper understanding of mathematics, verging on professional competence (at least for conceptual grasp, if not for manipulation of formulas). As my wife, Rhonda Roland Shearer, has demonstrated, Duchamp took particular interest in the work of the great mathematician Henri Poincaré, and much of his art represents a novel and systematic application of Poincaré’s views on the nature of time, space, causality, probability and even human creativity itself.
|
Click to enlarge
|
In 1967, Duchamp published, in an edition of 150 copies, a box containing facsimile reproductions of 79 notes, mostly compiled in the years just before World War I, and largely devoted to scientific subjects relevant to his plans for his greatest artistic work, The Large Glass. Scholars have not appreciated the scientific depth of these notes, but the forthcoming work of Shearer with New York University physicist Richard Brandt has revealed the genuine and explicit mathematical innovation within Duchamp’s rigorous analysis of four dimensional representation.
In a note that has attracted some scholarly attention (Figure 3), Duchamp penned an apparently cryptic metaphor about the fourth dimension. The “official” English translation, done by artist Cleve Gray under Duchamp’s personal supervision, states:
Two ‘similar’ objects, i.e. of different dimensions but one being the replica of the other (like 2 deckchairs [chaises ‘transatlantiques’ in the more expressive original French], one large and one doll size) could be used to establish a 4-dimensional perspective — not by placing them in relative positions with respect to each other in space3 [three dimensional space] but simply by considering the optical illusions produced by the difference in their dimensions.
|
Click to enlarge
|
 |
The reverse side of this note shows a fairly crude painting of three boats, depicted at varying distances from an observer based on clues provided by the enveloping landscape of trees, mountains and ponds (Figure 4). Since this naive little picture bears no evident relationship to Duchamp’s jottings on the reverse side, scholars have invariably assumed that Duchamp, following his usual procedure in writing important notes on the back of gas bills, beer coasters, etc., just used a scrap of paper immediately at hand when his muse struck.
For example, Duchamp scholar Francis Naumann states that many items in the White Box (the name of the 1967 publication) record “random notations… on a variety of topics, quickly jotted down on whatever writing surface happened to be available at the time. Several notes, for example, appear on gas bills dating from 1914, while others are written on the verso of postcards, photographs, advertisements, restaurant stationery, and other scraps of paper.” Naumann then explicitly placed the “deckchair” note in this category by claiming: “On the verso of a postcard, Duchamp also noted a possible means by which the fourth dimension could be visually established through a consideration of the optical illusion created by two deckchairs” — although neither Naumann, nor any other scholar, has ever tried to explain the actual nature of the illusion, presumably because they could not possibly decipher Duchamp’s note under the unquestioned assumption that the boats, as part of an irrelevant picture postcard, could be safely ignored as accidental and extraneous.
Duchamp’s object is not, in fact, a commercially produced postcard, but an original painting, almost surely by Duchamp himself, on a piece of paper presented, in his customary trickster’s way, in a humble guise that would keep its true nature invisible in plain sight. The reverse side (containing Duchamp’s note) also features a vertical line in the middle and four horizontal lines to the right, mimicking the address guides of a normal postcard. But these lines have been inked in by hand on this one-of-a-kind objet d’art. Why, then, did Duchamp draw lines at right angles to suggest the paraphernalia of a postcard? And why, more importantly, did he paint three boats on the picture side — and then write an apparently unrelated statement about deckchairs on the reverse?
The boats should have inspired at least a modicum of suspicion from the start. We assume, from conventional cues of perspective, that we see three boats of roughly the same length, but painted in different sizes to imply greater or lesser distance from an observer. The boats, on closer inspection, are a bit “funny” — but not sufficiently so to inspire much attention. Duchamp paints the visible part above the water in near bilateral symmetry with a supposed reflection in the water below. A yellowish (presumably metal) tip at the bow of each boat appears in such mirrored reflection, as does a human figure sitting upright in the middle of each boat. But what are we supposed to make of the rumpled gray material at the stern of each boat? A furled sail (but where, then, is the mast, and why does a little rowboat carry such a sail)? Or perhaps some blankets stored behind the human figure (but why as such a large and topheavy cargo)?
Serious attention to two common themes in Duchamp’s output neatly solves all these problems. First, as already stated, Duchamp delighted in concealing important statements (often on scientific themes) by depicting his original works as everyday commercial objects available in thousands of copies at ordinary stores. (In a subject for another time, Shearer has also discovered that none of Duchamp’s famous “readymades” really represent, as he claimed, factory-made objects signed by the artist, but otherwise unaltered, and thus reconfigured as art.)
Second, as scholars have documented in detail, and as the artist himself frequently noted with relish, Duchamp constantly played with the theme of 90 degree rotations in his art (see the accompanying 1965 photograph of Duchamp’s face seen simultaneously in profile and full view). Several motives underlie this preoccupation, ranging from an immediate and visceral delight in showing that visual “certainties” can often be discombobulated and reoriented by such a simple change, to the more abstract and technical reason that we represent an added mathematical dimension by an axis drawn at right angles (90 degrees) to all other axes — and that a right angle rotation therefore denotes (at least metaphorically) a view in a new dimension.
Shearer and I suspect, but cannot prove, that Duchamp had two motivations, one “sneaky” and the other quite overt (if we chose to see), for drawing those horizontal and vertical lines on the back of his boat painting: first, to fool us into regarding the work as a postcard; and second, to tell us, at the same time, that we must rotate the picture by 90 degrees to see both orientations of the optical illusion described in the note written over these orthogonal lines: one picture (the boats) in horizontal orientation — and another, representing the key to the whole work, by a 90 degree rotation into a vertical position.
|
Click to enlarge
|
Rhonda Shearer discovered this vertical key one evening as we indulged in our favorite pastime of playing mental chess with Duchampian puzzles. She turned the boats by the prescribed Duchampian 90 degrees (Figure 5) and we could only laugh at the gorgeous simplicity thus revealed, but so artfully, so craftfully (and craftily) hidden in plain sight. The three boats, seen entirely from the side as objects of similar size, but painted large or small to indicate relative distance from an observer in the inferred third dimension, become deckchairs, seen from above (in a bird’s eye view looking down), and necessarily interpreted as large or small (“large” and “doll size” in Duchamp’s words) because the picture, in vertical orientation, becomes entirely flat and two-dimensional when we lose the perspective cues (of pond and trees) needed to infer a third dimension of depth from a flat painting.
Now we can finally understand why the boats look a bit “funny” in the horizontal view: Duchamp included the odd features to make a plausible deckchair in 90 degree rotation! The metal tip at the boat’s bow becomes the wooden rod of the chair, projecting above the cloth seat and backing. The man in the boat becomes the arm of the chair, while the furled sails (or whatever we take the paraphernalia on the stern of the boat to represent) become the blanket to cover our legs on the windy deck of the Queen Mary.
In short, by a simple rotation of 90 degrees, a group of boats, seen entirely from the side and represented as near and far in three dimensions, becomes a group of deckchairs, seen entirely from the top and represented as big and little in two dimensions.
Cute, even clever — but what’s the point beyond some visceral amusement produced by imposing one man’s artistic dexterity upon everybody’s perceptual foibles? How, in particular, does this bit of colored frippery illuminate Duchamp’s statement that he had invented a new form of representation “to establish a four dimensional perspective” — a view into a higher world imbued with spatial freedom that we cannot “see” in our surrounding three dimensional universe of height, width and depth? Should we actually take Duchamp seriously and literally, or is he just screwing around again, using some highfalutin’ scientific language to inflate a jest, and to poke further fun at mathematical claims about grand and universal abstraction?
Let us give the artist some benefit of doubt, some credit for his acknowledged brilliance, by taking him seriously and assuming that we really do need to enter a 4-D space if we wish to perceive Duchamp’s weird 3-D “hybrid” object all at once — his amalgam of boats-near-and-far-seen-entirely-from-the-side and deckchairs-big-and-little-seen-entirely-from-the-top. We cannot see an object from two completely orthogonal (right-angled) vantage points at the same time in our everyday perceptual world of three dimensions. For such simultaneous viewing, we would need to observe two adjacent faces of a single cube at the same time — while looking at each of them absolutely face on! (We can see both faces of a cube at the same time if we observe them at an angle, say by looking straight at the edge between the faces and then viewing each face at a slope of 45 degrees from our line of sight. But, in our world of three dimensions, we cannot see an object entirely from the side and entirely from above at the same time.)
So how can we regard Duchamp’s hybrid boat-deckchair as a single coherent image in 4-D space? Duchamp’s own answer turns out to be formally correct: we can only see a three-dimensional object entirely from the side and entirely from above at the same time if we make our observations from the fourth dimension. Moreover, in unscrambling this paradox for us, Duchamp has provided a remarkable insight into this perennially fascinating and frustrating topic of higher dimensional worlds that we can conceptualize reasonably well, and characterize rigorously in mathematical terms — but that we cannot possibly “see” directly because we live in a universe where immediate perception only extends into three dimensions.
Hardly any subject exceeds the fourth dimension both in public fascination and in difficulty of conceptualization — hence our long pedagogic struggle to develop devices that can work as explanatory aids. No technique has ever bettered the classical route of making analogies from the transition between two and three dimensions, which we can grasp easily from direct experience, to the passage between three and four dimensions, where we have no direct experience at all. Flatland, written by the English cleric E.A. Abbott in 1884, remains the most effective and beloved classic in this genre. Let us therefore return to this standard source as we try to explicate Duchamp’s four-dimensional illusion.
When the Sphere visits Flatland right at the auspicious moment of transition into the third millennium at the inception of year 2000, he first tries to teach A Square about the third dimension by verbal argument. But A Square cannot comprehend such an expanded universe of higher dimensionality, so the Sphere tears him from the plane of Flatland and treats him to a view of his entire universe from “above” (a dimension previously inconceivable to A Square). Of course, A Square has learned the shapes of buildings and compatriots in his two-dimensional world, but he could only resolve these forms by laboriously working his way around their perimeters and measuring the sides and angles. However, from his new vantage point above his old world, A Square can see the entire form of each Flatland object all at once — a wondrously new vision that he can only conceive and express as seeing the “invisible inside” of things in one grand, full and instantaneous view.
But when A Square returns to Flatland, he discovers that he cannot convey his newfound knowledge to his countrymen, who persistently fail to conceive this expanded modality of sight. A Square tries various pedagogic devices, including metaphors about unobstructed views of totalities all at once (whereas his compatriots “know” perfectly well that one can only see part of an object’s periphery from any single vantage point in Flatland), and a motto — “Upward, not Northward” — that he intones to remind himself of a miraculous insight that may fade from concept and memory in his renewed confinement to Flatland.
Abbott hoped that we might understand the invisible fourth dimension by making a strict analogy to A Square’s abrupt “promotion” from two into three dimensions. Flatland remains one of the great classics of science fiction and mathematical pedagogy, but I think that Abbott made a tactical error in his explicit choice of analogies. Abbott stresses A Square’s struggle to verbalize his new and instantaneous view of each Flatland object, a miraculous novelty that A Square can only manage to describe as an ability to see into the “interior” of objects from a mysterious new vantage point called “above” (“upward, not northward”). By strict analogy, we should then try to conceptualize the fourth dimension as a place outside our ordinary space, from which we might peer into the interior of our bodies.
When I first read Flatland as a teenager, I became enthralled with this prospect, and I spent years trying to work through the analogy in an overly literal way — to no avail. But A Square’s best verbalization only represents a limit imposed by his customary perception, not an optimal way to express the promotion from three to four dimensions. I believe that Abbott’s pedagogical aims would have been better served if he had focused upon a different aspect of A Square’s enlarged vision from above the plane of Flatland — an aspect that translates into a better (and technically more accurate) analogy for moving from three to four dimensions. A Square not only sees the “inside” of Flatland objects from his new dimension. He also, and with just as much novelty, sees the entirety of Flatland objects all at once — whereas, in the conventional and limited plane of Flatland, he can only grasp this totally in time, by moving laboriously around the periphery of each object. And this ability to see an entirety all at once, rather than bit-by-bit in extended time — far more than A Square’s limited and idiosyncratic expression of his discovery as a new vision into the “inside” of objects — provides the key that can unlock the nature of a transition from our familiar three dimensional world into a rich but imperceptible domain of four dimensions, a world as foreign to our experience as the undescribable “above” to the citizens of Flatland.
Thus, to make the most fruitful analogy, we should say that, just as A Square could see the totality of two dimensional objects all at once from a third dimension above, so might we, from a fourth dimension outside the confines of our familiar three dimensional space, be able to see the entire surface of a three-dimensional object all at once. And this vision of “totality all at once” captures the aspect of four dimensional perspective that Duchamp so brilliantly tried to convey in his illusion of boats and deckchairs. We cannot see an entire cube from any single point of sight in three directions. Rather, we must move our eye around the cube in time, and then mentally integrate the full object by piecing together a set of partial visions. But, if we could look down upon a cube from a fourth dimension at right angles to each of the cube’s three dimensions, we would be able to see all six faces, all at once.
To emphasize this crucial point in at least a semitechnical way: We represent traditional three-dimensional space on three “mutually orthogonal” axes — that is, on three lines intersecting at a point, with each line perpendicular to each of the other two. If we place our eye along any of these axes, we will see a full view of the other two axes face on — and these two axes will define a plane in the next lower two-dimensional space. For example, when we look directly down one axis of a cube from above, we obtain a full view of the face of the cube defined by the other two axes crossing at right angles to form the plane of this face. Similarly and by extension (following the “Flatland” method of arguing by analogy), if we could (as we can’t in the world we know) draw an additional axis at right angles to each of the three axes of a conventional cube in 3-D space, and if we could then look down upon the cube from a vantage point right along this fourth axis, we would see the entire surface of the 3-D cube all at once (just as we see an entire 2-D face of the cube along a third axis perpendicular to these two). In other words, in a 4-D world, we wouldn’t need to spend time moving our eye all around the cube in order to see all parts of its surface (as we must do in our 3-D world). Rather, we would see the full surface of the cube all at once from the fourth dimension — not through the dark glass of a lower order of observation, but truly face to face.
|
Click to enlarge
|
 |
We can now “cash out” Duchamp’s brilliant insight about 4-D representation (while, at the same time, understanding his fascination with both the reality and the metaphorical meaning of rotations by 90 degrees — (Figure 6). Duchamp wants us to regard the boats and deckchairs as two alternative views of a single image (like the duck-rabbit in 2-D). But we cannot do so in our 3-D world because we cannot see both views at once. That is, the picture will not flip from one state to the other from any single point of sight because we can only access the two views sequentially in time, by rotating the object 90 degrees and then seeing deckchairs in the previous boats.
But, in a 4-D world, we could see both versions of the single “hybrid” 3-D object at the same time (as boats-entirely-from-the-side and deckchairs-entirely-from-the-top). To grasp the paradox, consider the boat view and the deckchair view as residing on two adjacent faces of a cube. When we look at either face straight on (that is, entirely from the side or entirely from above), we cannot see the other face at all in our 3-D world. But we can see both faces simultaneously, and each straight on, along the added axis of a 4-D representation.
|
Click to enlarge
|
 |
Duchamp then devises a wonderful analogy between this almost inconceivable prospect of seeing an entire 3-D object all at once, and something we can easily achieve with our analogous sensation of touch. Suppose we hold a small penknife firmly in one hand. We can touch the knife’s outer surface at all points simultaneously, and we can reconstruct the form of the object from these sensations — even though we cannot see all parts of the knife’s surface simultaneously from any single vantage point in a 3-D world. Now, Duchamp suggests, suppose we regard our simultaneous touch in 3-D as analogous to the possibility of simultaneous sight in 4-D. Then we will understand how we might “see” the entire surface of a 3-D object all at once. In another of his White Box notes, Duchamp writes: “The 3 dimensional vision of a plane P. corresponds in the continuum to a 4 dimensional grasp of which one can get an idea by holding a penknife clasped in one’s fist, for example.”(Figure 7)
|
Click to enlarge
|
 |
Duchamp clarifies the meaning of this note with two sketches. If one tries to see an entire object within a space of the same dimensionality as the object itself, one cannot do so all at once, but must move around the object, taking and integrating different views in sequence. Duchamp follows the Flatland procedure of 2-D analogy by writing in another White Box note:
“When I represent a 3-D space by means of a 3-D sphere (or a 3-D cube) I am comparable to a flat individual A who sees the section of a drawn plane P. The individual A can move to A1. He measures, while moving, the 4 sides if the quadrangle but at each stop he sees a projection of the quadrangle on an imaginary axis perpendicular to his visual ray.” (Figure 8) But if, as the second sketch shows, the 2-D observer can move into a third dimension above, then he can see the plane P all at once. Similarly, one can see the entire surface of a 3-D cube all at once from the 4th dimension, just as one can feel the entire surface of a penknife simultaneously.
Several other White Box notes reinforce this interpretation of the boat-deckchair hybrid as a representation in four dimensions, with the alternative states as different 3-D views that cannot be seen simultaneously in our 3-D world. Duchamp begins by posing the classic conundrum: “What is the meaning of this word 4th dimension since it does not have either tactile or sensorial correspondence as do the 1st, the 2nd, the 3rd dimension.”
Duchamp then gives a wonderfully concise and generalized description of the boat-deckchair: “From the 2-dimensional perspective giving the appearance of the 3-dimensional continuum, construct a 3-dimensional (or perhaps a 2-dimensional perspective) of this 4-dimensional continuum.” This note sounds cryptic, but concrete translation into the boat-deckchair example resolves both meaning and intent: consider the boat and deckchair views as 2-D paintings that, at least for the boats (given the included cues for perspective), depict a world in 3-D. But both views really represent two aspects of a “hybrid” 3-D object seen simultaneously in 4-D space. We can now finally grasp what Duchamp meant when he wrote, on the back of the boat “pseudopostcard” (as quoted earlier in this essay): ” . . . to establish a 4-dimensional perspective — not by placing them in relative positions with respect to each other in space³ but simply by considering the optical illusions produced by the difference in their dimensions.”
We also know that Duchamp invoked the example of a 3-D cube to express the simultaneous view of an entire 3-D object in 4-D space — thus representing the boat-deckchair duality as two views on two adjacent faces of a cube, both visible at the same time in 4-D. Duchamp describes this simultaneous sight of the entire cube, again making an analogy to simultaneous touch of the penknife in 3-D (I love his phrase “circum-hyperhypo-embraced” — that is, “grasped all around at once, both above and below”): 3-D perspective starts in an initial frontal plane without deformation. 4-D perspective will have a cube or 3-D medium as a starting point which will not cause deformation, i.e. in which the 3-D object is seen circum-hyperhypo-embraced (as if grasped with the hand and not seen with the eyes).
Finally, Duchamp explicitly notes that, in 4-D space, two intersecting planes (the boats and the deckchairs on two adjacent faces of a cube) can be seen at once along an axis in the higher dimension: “2 intersecting planes do not determine a space — they merge along a plane perpendicular to their common intersecting line.”
Popular books on the 4th dimension often try to depict this additional factor as time, while treating the three dimensions of our everyday world as space. This common formulation expresses Duchamp’s observation that, in ordinary 3-D space, one can only “see” the entirety of an object through time — because one must move one’s eye sequentially around a 3-D object to grasp the full form that can’t be perceived all at once. But we can express both the paradox and the reality of the 4th dimension in a more interesting (and also mathematically accurate) manner when we represent the added dimension spatially — as a fourth axis (albeit undrawable in our surrounding 3-D world) at right angles to each of our three everyday spatial axes, and therefore imbued with the wondrous property of offering a simultaneous view of entire 3-D objects — if only we could leave our 3-D world and, like A Square above the plane of Flatland, gaze upon our known universe from outside.
Such a prospect must stand as the most exciting symbol, and the most thrilling potential realization (if we could ever find the exit from our 3-D prison), for the grandest goal, the summum bonum, of our mental lives and dreams — transcendence to a higher and genuine (not a fuzzily metaphorical) view of reality. Duchamp’s 4-D boat-deckchair therefore embodies both our fondest dreams and our deepest intellectual struggles in a perfectly lovely and humble item of four dimensional concrete.
But the eurekas of millennial transitions to higher dimensions of insight pose as many present dangers as potential rewards. A Square, Abbott’s hero of the year 2000, ends up in prison, condemned as a dangerous radical who, like Socrates, might corrupt the youth if allowed to roam free and preach “the gospel of three dimension.” As Duchamp reminds us more gently, and with sophisticated and cryptic humor, we also live within a maze of conceptual prisons that might hold us even more tightly because we do not perceive the walls. But if we could find the entrance to an expanded world where boats and deckchairs fuse into one point of sight, then these walls might also enter our field of vision — and we might greet this insight with a bellow of joy exceeding the vocal power of Joshua’s entire army, as they shouted and trumpeted so many years ago at Jericho, when the walls came a-tumbling down!(9)
This essay has been published simultaneously in the December 1999 issue of Natural History Magazine 10, vol. 10 (December 1999 / January 2000), pp.32-44.
Notes
 1.from: J.R. Block and Harold E. Yucker, Can You Believe Your Eyes?, New York: Gardner, 1989, p. 16, fig. 2.2
1.from: J.R. Block and Harold E. Yucker, Can You Believe Your Eyes?, New York: Gardner, 1989, p. 16, fig. 2.2
 2.from: J.R. Block and Harold E. Yucker, Can You Believe Your Eyes?, New
2.from: J.R. Block and Harold E. Yucker, Can You Believe Your Eyes?, New
York: Gardner, 1989, p. 16, fig. 2.2
 3.from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier
3.from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier
& Ekstrom, 1967 [plexiglass box of 79 facsimile notes (translated by Cleve Gray) concerning The Large Glass; signed and numbered edition of 150]
 4. from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier & Ekstrom, 1967 [plexiglass box of 79 facsimile notes (translated by Cleve Gray) concerning The Large Glass; signed and numbered edition of 150]
4. from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier & Ekstrom, 1967 [plexiglass box of 79 facsimile notes (translated by Cleve Gray) concerning The Large Glass; signed and numbered edition of 150]
 5. from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier & Ekstrom, 1967 [plexiglass box of 79 facsimile notes (translated by Cleve Gray) concerning The Large Glass; signed and numbered edition of 150]
5. from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier & Ekstrom, 1967 [plexiglass box of 79 facsimile notes (translated by Cleve Gray) concerning The Large Glass; signed and numbered edition of 150]
 6. cover of Robert Lebel’s Marcel Duchamp, Paris: Trianon, 1959 (first monograph and catalogue raisonné of the artist); photograph by Victor Obsatz
6. cover of Robert Lebel’s Marcel Duchamp, Paris: Trianon, 1959 (first monograph and catalogue raisonné of the artist); photograph by Victor Obsatz

7. from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier & Ekstrom, 1967 [plexiglass box of 79 facsimile notes (translated by Cleve Gray) concerning The Large Glass; signed and numbered edition of 150]
 8. from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier & Ekstrom, 1967 [plexiglass box of 79 facsimile notes (translated by Cleve Gray) concerning The Large Glass; signed and numbered edition of 150]
8. from: Marcel Duchamp, A l’Infinitif (The White Box), New York: Cordier & Ekstrom, 1967 [plexiglass box of 79 facsimile notes (translated by Cleve Gray) concerning The Large Glass; signed and numbered edition of 150]
 9.My wife and I wrote this essay for the millennial issue (December 1999-January 2000) of Natural History. In treating this grandest temporal passage in all our lives, I wanted to follow the essayist’s fundamental principle of using a particular example to illustrate a broad generality — in this case the nature and overarching value of expanded mental horizons — that no one but an arrogant fool would attack head on. (An explicit essay about “the nature of truth” merits only our instant and a priori ridicule). Duchamp’s brilliant and entirely misunderstood four-dimensional perspective illusion of boats and deckchairs works well as such a concrete illustration, especially since I could amalgamate his story with the best fictional invocation, written more than a century ago in 1884, of the forecoming (and now passing) 1999-2000 millennial transition as a symbol for the possibility (and both the difficulty and danger, for the hero of this tale ends up scorned and in prison) of discovering fundamentally new dimensions in human and scientific understanding. Incidentally, I have stated that I will end this series of essays at the Millennium (right on number 300, with never a month missed since 1974, and following the admirable DiMaggio-Jordan principle of quitting while ahead). Please don’t regard the forthcoming and final year of these essays as a retreat from this pledge, analogous to the almost comical image of a diva’s multiple “farewell” tours. As I discussed at length in my book Questioning the Millennium, perfectly good defenses can be advanced for either a 2000 or a 2001 beginning for the 3rd millennium. I happen to maintain a slight preference for 2000 (as did the good Reverend E.A. Abbot in 1884), while acknowledging that both positions enjoy undeniable merit as consequences of arbitrary human decisions that cannot be validated, or disconfirmed, by scientific knowledge. Nonetheless, as a practical point, I will write until January 2001 (as I always had intended) — because it would be such a shame to make a big fuss about quitting at the millennium, only to face the possibility that partisans of 2001 will triumph in the public debate — and that posterity will judge me as falling short, just before the finish line. I have always followed my grandfather’s rules for a successful life: Hedge your bets and never draw to an inside straight. You will have me to kick around only for one more year.
9.My wife and I wrote this essay for the millennial issue (December 1999-January 2000) of Natural History. In treating this grandest temporal passage in all our lives, I wanted to follow the essayist’s fundamental principle of using a particular example to illustrate a broad generality — in this case the nature and overarching value of expanded mental horizons — that no one but an arrogant fool would attack head on. (An explicit essay about “the nature of truth” merits only our instant and a priori ridicule). Duchamp’s brilliant and entirely misunderstood four-dimensional perspective illusion of boats and deckchairs works well as such a concrete illustration, especially since I could amalgamate his story with the best fictional invocation, written more than a century ago in 1884, of the forecoming (and now passing) 1999-2000 millennial transition as a symbol for the possibility (and both the difficulty and danger, for the hero of this tale ends up scorned and in prison) of discovering fundamentally new dimensions in human and scientific understanding. Incidentally, I have stated that I will end this series of essays at the Millennium (right on number 300, with never a month missed since 1974, and following the admirable DiMaggio-Jordan principle of quitting while ahead). Please don’t regard the forthcoming and final year of these essays as a retreat from this pledge, analogous to the almost comical image of a diva’s multiple “farewell” tours. As I discussed at length in my book Questioning the Millennium, perfectly good defenses can be advanced for either a 2000 or a 2001 beginning for the 3rd millennium. I happen to maintain a slight preference for 2000 (as did the good Reverend E.A. Abbot in 1884), while acknowledging that both positions enjoy undeniable merit as consequences of arbitrary human decisions that cannot be validated, or disconfirmed, by scientific knowledge. Nonetheless, as a practical point, I will write until January 2001 (as I always had intended) — because it would be such a shame to make a big fuss about quitting at the millennium, only to face the possibility that partisans of 2001 will triumph in the public debate — and that posterity will judge me as falling short, just before the finish line. I have always followed my grandfather’s rules for a successful life: Hedge your bets and never draw to an inside straight. You will have me to kick around only for one more year.
Fig.3~8 © 1999 Succession Marcel Duchamp, ARS, N.Y./ADAGP, Paris.







