click to enlarge
Figure 39	Figure 40
M. C. Escher, Another world II, 1947	Paul klee, Perspective with inhabitant, 1921

What I said so far shows clearly that the theme of the impossible 3D objects and the one of an enlarged conception of the perspective are tightly linked to each other. Thus I want just to recall some of Escher’s experiments on perspective which Klee and Duchamp also did with similar outcomes.

In Escher’s Another world II (1947) (Fig. 39) the only vanishing point (roughly in the center of the print) must be considered at once on the horizon, or at the zenith or at the nadir, depending on which bird (and which wall) we are considering. The same holds for Klee’s Perspective with inhabitants (1921) (Fig. 40).

In Relativity (1953) (Fig. 41) Escher needed three distinct vanishing points to represent a world with three different gravitational fields, where people can walk on the walls as well as on the floor or the ceiling. In Klee’s Arab town (1922) (Fig. 42) we see a similar effect: the ground plane containing the floor of the higher part of the painting is the same plane containing the back walls in the lower part.

The fluid perspective in Escher’s House of stairs (1951) (Fig. 43) could be also explained by Klee’s idea of a stray viewpoint, and the final outcome could be compared with the one of Soaring.

click to enlarge
Figure 41	Figure 42	Figure 43
M. C. Escher, Relativity, 1953	Paul Klee, Arab Town, 1922	M. C. Escher, House of Stairs , 1951

Finally, as far as Duchamp’s perspective experiments are concerned, Shearer [rrs4]   showed a quantity of different perspective tricks devised by Duchamp, ranging from stray viewpoints, multiple vanishing points, fluid perspective, photographic overlapping, and so on ⁽²⁶⁾. Of course, they maintain an high degree of similarity with the ones of Escher and Klee.

Let’s now return to the impossible objects, and see them from another viewpoint.

click to enlarge

Figure 44

M. C. Escher, Waterfall, 1961

Sketch 15

The simple tribar underling the building of Waterfall

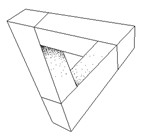
What do they represent? Especially in Escher’s case it is evident that they are variation on a leitmotiv: the one of perpetuum mobile. Look at Waterfall (1961) (Fig. 44) or even at Ascending and Descending, which explicitly show endless motions. But look even at the simple tribar (Sketch 15) which underlies the building of Waterfall. As we go with the eye along its bars, we perceive a sense of depth, we feel we are leaving the plane where the bars are actually drawn, to enter in the third dimension; and the pathway is really endless because, once the turn is completed, we can repeat it again and again; every time we find ourselves at the starting point.

Thus the impossible objects belong to a world which isn’t subjected to the law of thermodynamics: here entropy doesn’t increase, but reduces itself, to allow perpetual motions, such as in Waterfall. 

A similar overturning is exactly what happens in complex systems with self-organization, which is one of the key concept in complexity sciences. Self-organization means that a system, provided certain conditions (one of them being the complexity of the system itself) spontaneously reduces its entropy, by introducing new levels of order among its elements. The slogan coined by Stuart Kauffman ⁽²⁷⁾, Order for free, effectively captures the essence of the stunning and seemingly paradoxical discover of a self-established order.

Now, if Klee, Duchamp and Escher guessed something about self organization as I believe and as I tried to highlight, then the impossible objects in a way could express with their paradoxical properties the surprising order-for-free nature of complex systems.

After all, something similar has been already said by Jean Clair about the Glass:

Michel Carruoges ⁽²⁸⁾ noticed that the intricate machinery of the Glass shows several analogies with other imaginary machines and engines, devised in same period by Jarry, Roussel, Kafka… Several years after, Jean Clair ⁽²⁹⁾ recalled Carrouges’ statement, and further deepened the parallelism, including in the list a quantity of pseudoscientific inventions which were popular in those years. One of the leitmotivs of those peculiar machines (Glass included) was that they produce more energy than they use, said Clair, thus they are variations on the theme of the perpetuum mobile. In fact they overturn the reality principle (the second law of thermodynamics) into the pleasure principle (the dream of an energy completely free and available).

In short, in my way of seeing things, we can group impossible objects and these machines together.

click to enlarge

Sketch 16

Necker Cube

But a further connection can also be found, particularly referred to the Necker Cube (Sketch 16), which underlies several impossible objects, such as the Impossible Bed of Apolinaire enameled. Indeed, as Rosen ⁽³⁰⁾ observed, the Necker Cube encompasses within itself, thus we can connect it to the same themes we discussed for the self-encompassing topological figures: hence feedback looping and self-reference.

5. A unifying reading perspective

In conclusion, I would like to delimit the context in which this paper should be read.

Often it happens that many people at once, unconsciously, independently and following different courses, elaborate the same new ideas and concepts, and help cement them into the Zeitgeist. In fact they contribute to the emergence of new sensibilities and new ways of observing, interpreting and understanding the world. This was the case for Klee, Duchamp and Escher: I believe they expressed (being in advance on their time) and contributed towards ideas that would grow and be affirmed. Nowadays, this new paradigm, this new way of seeing things is expressed by the so called complexity sciences.

Reiner Hedrich ⁽³¹⁾ stressed some salient traits in the development of complexity sciences. Here I’m interested in two of them. First, the gestation period of the new theories has been very long, about one hundred years. This long latency period, necessary to find a solid mathematical theory useful to describe dynamic systems behavior generously covers the lifetimes of Klee, Duchamp and Escher. Thus, in a way, they were immersed in a stream of ideas and concepts which were still under construction and organizing in theories. I’m talking about a nascient stream in the cultural subconscious, not one that was flowing on the surface of the well established scientific culture of those years; thus I don’t think that our artists could have been directly influenced by those scientific ideas; generally speaking, even admitting the possibility of such an exchange of views, in my opinion it is easier to think it happened in the opposite direction. With a few exceptions: for some aspects (I think of concepts such as instabilities and chaos) scholars acknowledge Duchamp has been influenced by the reading of Poincaré; but they are just only some aspects of his complex thought; the same holds for Klee’s possible understanding of (evolutionary) biology and natural sciences, or for the mathematical readings of Escher, which moreover in some cases he admitted to be unable to understand. The second feature in the development of complexity sciences stressed by Hedrich is that the grounding ideas of the new paradigm, the kernel of complexity, didn’t deal with a specific disciplinary field: instead, they are a sort of conceptual foundation, a shared background for any empirical discipline dealing with complex systems. This fact makes it conceivable that there was, to some extent, a widespread and unconscious emergence of such ideas, even though in purely qualitative and intuitive terms. In other words, I’m talking about quite general concepts, and not about specific subjects or details of a well-defined disciplinary field: it makes possible that the same ideas could have been grasped by someone in more intuitive forms, which is what I’m suggesting for Klee, Duchamp and Escher.

The concepts I’m talking about are closely related to each other, they form a tangle of interconnected ideas, that bringing one of them to the light, mostly implies that many (or even all of) the others could also somehow come out. Really, it is impossible to examine thoroughly one of them without revealing a cascade connection with each other. Indeed, the idea of cyclic dynamism of a system entails feedback, recursion and self-reference; in turn self-organization, fractals and chaos are entailed, and again emergence, dynamic and unstable equilibria, (co)evolution; further, the visual expression of such a complexity needs new and different ways to conceive the space, where new and more complex relations may occur between its elements; thus, the represented space has strange topological properties.

It is well-known that complexity introduces several relevant changes in the way we used to know the world. This is not the place to discuss them: I’ll limit myself to summarizing some of them.

First: mainly due to both deterministic chaos and sensitive dependence on the initial conditions which characterize the dynamical systems, we have to accept two weaker versions of both the causality principle and determinism.

click to enlarge

Sketch 17

Diagram explaining concept of complexity

Second: because of the concept of emergence, the reductionist approach is not more suitable to study complex systems. This is sometime expressed by opposing reductionism and holism. I like the way Chris Langton expresses the concept by means of Sketch 17 which I took from Roger Lewin ⁽³²⁾.

To effectively explain the radical change in the way of seeing the world implied by complexity, a set of dichotomies is often used, which confronts old paradigms with new:

simplicity-complexity, reductionism-holism, determinism-uncertainty, quantity-quality, necessity-contingence, predictability-unpredictability, reversibility-irreversibility, repeatability-unrepeatability, causality-randomness, law-chaos… Interestingly, if we attempt to describe Klee, Duchamp and Escher by choosing either of the poles in such dichotomies, we always have to choose the second one.

As far as Duchamp is concerned, the discussion about the crisis of determinism and reductionism has been already widely discussed, particularly in relation to the ideas of Poincaré’s .

Coming to Klee, I want just recall his essay titled Exact experiences in the field of art ⁽³³⁾, where he expressed a concept which is one of the leitmotiv of his activity as both artist and teacher: the freedom and the intuition of the artist act in the space between law and unpredictability, but always remembering the necessity of both:

Oh, don't let the eternal spark become completely smothered by law's measure! Take steps in time! But don't go away from this world completely. ⁽³⁴⁾

Escher expressed a similar ambivalence with his prints, in the paradoxical coexistence of extreme formal rigor and uncertainty, mathematical exactness and instability, rigorous application of exact principles and unpredictability in the outcomes.

On the other hand, only a few words are needed to recall that Klee, Duchamp and Escher built their work as organisms, composed by a number of interacting elements, where the whole is always greater than the sum of its parts. In their works complex processes are mostly represented, whose outcomes can be emergent, unexpected properties. We can dissect them, but in so doing we always lose something. This is the true essence of their holistic art.