Complexity Art by Roberto Giunti |
|||||||||||||||||||||||||||||||||||||||||||||
|
Returning now to Klee’s Conqueror, it is easy to see similar treatments in its banner. Especially in this case, as we said above, the perception oscillates continually between the 2D and 3D: no sooner have we arrived at a 2D hypothesis, then we are pushed to reject it and embrace 3D one, and vice versa. The relevance of some of Duchamp’s and Escher's ideas is here clear, for it is well-known that the conflict between surface and space is one of the most important among their themes.
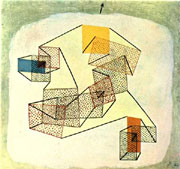
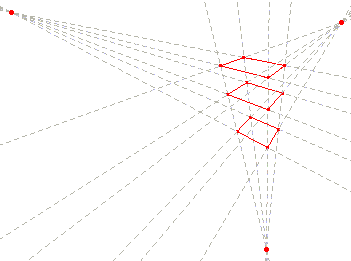
Let’s now turn our attention to Klee’s Soaring, Before the Ascension (1930) (Fig. 34) which is representative of several paintings based on the same framework, worked out in the years we are considering. The framework is based on rectangles freely soaring over the whole surface of the work, connected to each other with colored bars. At the first glance we realize that the whole is spatially inconsistent, though the local details are not. Particularly, it happens that focusing our attention on a couple of connected rectangles at once, there is no problem; but considering three or more connected rectangles at once, in the most cases it yields spatial inconsistencies, that prevent the observer from seeing which are the closest or the farthest planes (unless one admits the bars could make a hole in the rectangles and pass through them). In Soaring
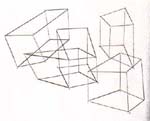
Klee used several skewed perspective boxes at once, like the ones in
his pedagogical sketch (Sketch 9). Here
we are confronted with the desired effect of spatial ambiguity, for
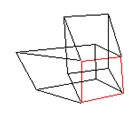
a face (the red one in see Sketch 10) might
simultaneously belong to several boxes, each of them suggesting a different
perspective; thus, that face has an ambiguous spatial collocation. We
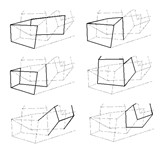
can easily see the practical effects of such a strategy in Sketch
11, which displays several of the possible simultaneous perspectives
contained in a single detail of Soaring. Interestingly, because
of their shared surfaces, the perspective boxes used by Klee form a
wide network of connected elements. Notice: not just a linear chain
of elements, but a true net, which allows a multiplicity of possible
circular courses (22).
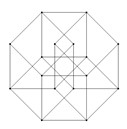
This kind of construction makes me think to something like the hypercube displayed in Sketch 12 and this of course recalls the Duchamp’s pet; the fourth dimension. Thus, look at Poster for the Third Chess Championship (1925) (Fig. 35), where Rhonda Shearer (23) showed several analogous spatial inconsistencies. One of the most
famous 3D impossible objects of Escher’s is Ascending and Descending
(1960) (Fig. 36): on the roof of a building
we see an endless staircase. Once again we have a circular course ever
returning to its starting point. It is well-known, and Bruno Ernst (24)
explained it carefully, that the building, which has the impossible
staircase on its roof, has a strange perspective structure, shown in
Sketch 13. More than any verbal explanation,
animations 3 and 4 help us understand the key reason for this. Animation
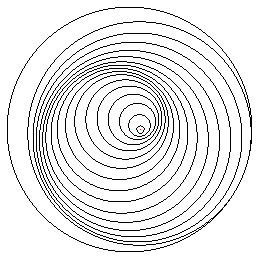
3 is a perspective sketch with one only vanishing point.
It starts by showing three distinct parallel planes. They are perspectively
represented with three closed polygonal lines (namely three rectangles)
whose edges are of course not connected with each other. But
by slightly rotating one of the edges of the optical pyramid around
the vanishing point, we get a spiraling polygon, which joins in a single
connected line the edges of several planes. The same holds if perspective
has three vanishing points: look at Animation 4,
which explains the perspective structure of Escher’s impossible building.
Here is the surprise. Look at Sketch 14:
the impossible room in Klee’s Chess is based just on the construction
presented in animation 3, thus it is deeply linked to the impossible
building of Escher’s Ascending and descending. (Further explanation
for this can be found in the article cited above (25)).
Thus, in these cases both Klee and Escher conceived perspective in terms of an iterative process, whose outcome is the spiraling, growing motion we saw in their buildings, as well as in a nautilus shell; thus they thought of the vanishing point as a sort of attractor of a dynamic system.
Can we see anything of this in Duchamp’s work? Not exactly the same, but in a way the answer is: yes, there are. One of the major achievements of Duchamp on perspective is of course the lower half of the Glass (we shall consider the Completed Large Glass, 1965 (Fig. 37)). Thus, look at the Slide, a perfect perspective box which contains the rotatory element named the Water mill. Many other rotatory elements can also be found in the lower part of the Glass, such as the Chocolate grinder or the Oculist chards, but particularly the pathway described by the Sieves or the Toboggan have the feature of a spiral shell we are interested in. The analogy between these elements and the perspective spirals we saw above is admittedly weak. But look now at Rotary demisphere (1925) (Fig. 38). Animation 5 can help visualize the surprising perspective depth effect one yields once a similar device is rotating. This is quite close to Klee's and Escher's idea of considering the perspective vanishing point as a sort of attractor of an iterative process which implies spiral motions. >>Next
Notes
The framework of Soaring is just the first important achievement of such a creative course, which will lead in the late works to the theme of morphogenesis.
Figs.
35, 37-38
|
|||||||||||||||||||||||||||||||||||||||||||||