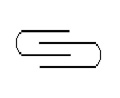
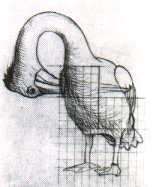
Jean Clair ⁽¹⁷⁾ suggested an interesting analogy between the kleinian bottle and some alchemic symbols, such as the one of the pelican devouring itself, and then he connected it with Duchamp’s Air de Paris (Fig. 24). Look now at Escher’s preparatory sketch (Sketch 3) of a Pelican; although in the definitive print he substituted the pelican with a dragon (Dragon, 1952) (Fig. 25), he maintained however the same idea of a self-penetrating and self-eating animal (after all, the snakes eating each other’s tail in Moebius band I refer to the same theme). As far as Klee is concerned, we saw similar self-eating structures, though abstract, in the meandering lines of the drawings around 1934, use the same techniques as the previously mentioned Excited: the basic motif (see Sketch 4) is formed by two curves penetrating one another, the end of the one into the belly of the other.

click to enlarge
Figure 24	Figure 25
Marcel Duchamp, Air de Paris, 1919	M. C. Escher, Dragon, 1952
Sketch 3	Sketch 4
M. C. Escher, preparatory sketch of a Pelican	Two curves penetrating one another

In his latest style Klee used a typical pattern whose genesis and meaning we can better understand by looking at a detail of the drawing The fugitive is Looking Back (1939) (Fig. 26); the body of the fugitive is based on branching curved lines, the one starting from the back of another. The head too is formed by a similar, curved line, but it is branching from its own back, in a circular, self-referential scheme. This motif is further amplified in innumerable drawings and paintings around 1939-40, where we find a lot of self-embedded, self-encompassed figures, such as in Fastening (1939) (Fig. 27).

Figure 26	Figure 27
Paul Klee, The fugitive is Looking Back, 1939	Paul Klee, Fastening, 1939

What is the significance of this trend for using topological figures? What relationship can we establish between that and complexity?

First, with Klee, Duchamp and Escher there is a tendency to represent very complex things, where the parts are widely connected to each other, interacting with non-linear pathways, often looping and returning to some crucial points. Thus the tangled intricacy of some knots or labyrinths visually and effectively expresses the corresponding intricacy of the components of their complex systems.

Second, such intricacy of connections within a system often produces unexpected outcomes, which in turn imply new unexpected outcomes, and so on. Thus in the complex system represented in their works by our artists, it is difficult to discern clearly causes and effects, because of the network of their reciprocal feedback. The unexpected, often strange and sometimes paradoxical outcomes  rising from systems subjected to circular feedback and self-referential loops have corresponded with the strange and paradoxical properties of figures such as knots, the Moebius strip or the Kleinian bottle, due to their circularity, their self-intersections or self-penetrations. The same could be said for those figures discussed above, often used by the late Klee, which are self-encompassing.

Particularly in the case of Duchamp, as I have already shown ⁽¹⁸⁾, the topological properties of the kleinian bottle were used to express the paradoxical identity Egg-Mother (or Bride-Glass). This was discussed in the previous section, and in general to express the autopoetic properties of the duo Glass-Box.

4. Enlarged perspective and Impossible 3D objects

click to enlarge

Figure 28

Marcel Duchamp, Apolinère Enameled, 1916-17

Figure 29

Paul Klee, Chess, 1931

Sketch 5

Trihedral junction versus Dihedral T-junction

Sketch 6

Trihedral junction versus Dihedral T-junction in Apolinère Enameled

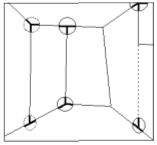
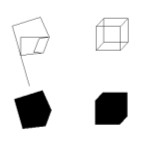
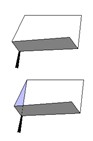
Rhonda Shearer [rrs3]  ⁽¹⁹⁾ thoroughly discussed the relationship between some of Eschers’ and Duchamps’ works, based on 3D impossible objects. She documented how Duchamp’s Apolinère Enameled (1916-17) (Fig. 28) predates by forty years the seminal paper of Lionel and Roger Penrose on impossible 3D figures ⁽²⁰⁾. She also stresses the bond of friendship between Duchamp and Roland Penrose, a close relative of Lionel and Roger. The cited Penrose article is the professed source of inspiration of Escher’s famous impossible figures, so that the reading of Shearer’s article cements a direct link between Escher and Duchamp via the Penroses.

But, what about Klee’s impossible 3D objects? We shall discuss some works, which are representative of corresponding frameworks, all of them developed in about 1930 and deeply linked with one another.

The first we shall consider is Chess (1931) (Fig. 29). I have elsewhere already examined this painting, its genesis and its possible meaning ⁽²¹⁾. Here I want only to recall that the bare, empty room in the background is an impossible 3D object (as a matter of fact, many other elements in the painting are spatially inconsistent, but here we shall confine ourselves to the background only).

The walls of the room are joined to each other by means of vertical edges, three of which are explicitly traced, whilst the fourth (the dotted one in Sketch 5) is only suggested by the left side of the paler rectangle in the upper right hand corner of the painting. Three of those vertical edges have mutually inconsistent junctions at the opposite extremities: one end shows a trihedral junction, where three distinct edges converge, while at the opposite end, two of the three edges line up one another, giving rise to a dihedral T-junction. Thus, the background is an impossible, puzzling 3D object, and the checkerboard covering over the scene may suggest something like a chess problem, just to emphasize the spatial enigma posed by the background.

Look now at Apolinère Enameled: one among the ingredients for making this 3D object impossible, is just the same as for Klee’s Chess: mutually inconsistent ends of a edge, highlighted in Sketch 6.

Klee used to express the concepts and the ideas he was interested in, by means of graphic simplifications, focusing his attention on only the essential parts. He would discard irrelevant and non-essential details, that might mislead the observer and would especially avoid repetition and redundancy. If necessary they wold just suggested.

That’s the reason why we find traces of other impossible 3D objects in a very simplified form; as is the case for The Conqueror (1930) (Fig. 30). Look at his banner. Though a banner is essentially a flat object, at first sight we actually perceive something like a cube, a solid figure; but counting the peripheral sides of the overall silhouette, we find that there are five, not six, as we would generally expect (Sketch 7). Something here is wrong: as soon as we accept the hypothesis of a possible 3D vision, we immediately recognize that it is inconsistent with some details of the motif. There is something missing. To better understand what really is missing, let us examine a further simplified versions of the same motif in another of Klees’ pictures: Six species (1930) (Fig. 31). Look at the flower displayed in Sketch 8. To make it spatially plausible, we have to mentally add a missing edge to form a trihedron; the same holds of course for each other flower in the painting. Without the addition of the missing edge we perceive something oscillating between a dihedron and a trihedron, which leads us back to the analogous ambiguity we saw in Chess.

click to enlarge
Figure 30	Figure 31
Paul Klee, The Conqueror, 1930	Paul Klee, Six Species, 1930
Sketch 7	Sketch 8
The impossible 3D object	An edge is added to form a trihedron

Notice now that Duchamp was interested in exactly the same ambiguity. Look indeed at the recto side of the Hershey Postcard note (circa 1915) (Fig. 32), or even at the miniature reproduction of Why Not Sneeze Rose Sélavy? in the Boite-en-Valise (1941) (Fig. 33). >>Next

click to enlarge
Figure 32	Figure 33
Marcel Duchamp, Note on Hershey Postcard, circa 1915	Marcel Duchamp, miniature version of Why Not Sneeze Rose Sélavy? (1921), in Boite-en-Valise (1941)

Figs. 24, 28, 32-33
©2003 Succession Marcel Duchamp, ARS, N.Y./ADAGP, Paris. All rights reserved.