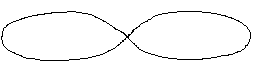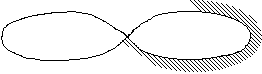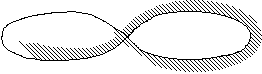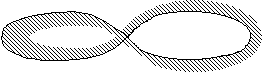Complexity Art by Roberto Giunti |
|||||||||||||||||||||||||||||||||||||
|
3. Topology
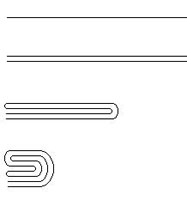
Klee, Duchamp and Escher were all three attracted by topologically interesting figures. Several of Escher’s works deal with topological figures, such as knots (Knots, 1965) and Moebius strips (as in Moebius band I, 1961 (Fig. 14) and Moebius band II, 1963 (Fig. 15)). Moebius strips (see Animation 1 which explains a possible genesis of the strip starting from a cylinder) exhibit a number of interesting properties; I’ll recall and briefly explain some of them. First, unlike the cylinder, which has both an internal and external surface, the Moebius strip has only one surface; This can be easily verified by mentally painting its whole surface, without lifting the brush from the strip. Second, whilst a cylinder has two edges (lower and higher) the Moebius strip has one only edge; once again you can follow this edge completely with the finger without having to lift it from the edge. Furthermore, if one cuts the cylinder longitudinally, two distinct cylinders will be obtained, whereas by cutting the Moebius strip the same way, one only new strip is yielded. Escher carefully showed these properties in his prints. In Moebius band I he cut the strip longitudinally and obtained three snakes eating each other’s tail, while in Moebius band II nine ants in line walk on the strip, so as to highlight the single edge and single face concepts. Escher was interested in the circularity of his knots and strips. He drew them together in a monograph (12) under the chapter heading spatial circles and spirals. His knots, Moebius strips, as well as planar and spherical spirals, were all drawn together in this section. The knots follow circular pathways which end up at the starting point after torsions and self-intersections. The same holds for the Moebius strips. Klee too, was
interested in knots, and had been since childhood. Several of his early
drawings show knotted worms hanging from a fisherman’s hook. We see
the same worms, now abstract knots, in later drawings such as Ways
Toward the Knot (1930) (Fig. 16).
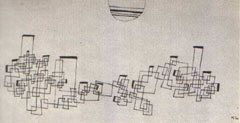
2D knots are also drawn according to even more essential forms, like
the infinity-shaped motif (and its polygonal variants) shown in his
pedagogical sketch (see Sketch 1). We see
a huge collection of similar patterns in pictures like Dynamically
polyphonic group (1931) (Fig. 17),
which is based on a feature of those 2D knots Klee was interested in
(see Animation 2): a hatch follows the
course of the knot with continuity, but always remaining on the same
side of the line; in so doing, the hatch highlights the inside of one
half of the motif, and the outside of the other half. How is it possible
to pass from inside to outside, while remaining on the same side of
the line? It is due to the self-intersection of the 2D knot (corresponding
with the torsion in the Moebius strip), which allows passage
from an inner to an outer region, without passing from one side of
the line to the other. As we saw before, Moebius strip has a similar
property. Let us return to Klee’s 2D knots. He amplified them, to form
complex, perpetual pathways, once again formed by uninterrupted, closed,
self-intersecting lines (often polygonal instead of curved) and always
returning to the starting point. This is typical of Klee’s drawings
of the late 20’s and the early 30’s. An example is the drawing Mechanics
of an Urban Area (1928) (Fig. 18).
We have other evidence of the special topological meaning of Klee’s images, such as labyrinths. Labyrinthine lines and signs are indeed among the most important patterns in Klee’s late style. Several hypotheses could be made to explain the genesis of such patterns, and in my opinion they are often linked to morphogenetic processes (13). There are, however, some drawings, such as Excited (1934) (Fig. 19) and all the others, based on the same framework, which particularly show the underlying presence of the folding recursive process (see Sketch 2). Similar (but reversed) processes are sometime used for classifying labyrinths in topology (14) unrolling them, to obtain the simpler equivalent form. But, interestingly, similar folding processes can also give rise to fractal and/or chaotic structures (15) which in turn can be connected with the corresponding themes highlighted above. With reference to the use of Duchamp’s topological figures, I have already underlined the importance of the Kleinian bottle, along with some related Moebius-strip-like structures in his writings and works (16), and I have already stressed a possible meaning of this circular self-penetrating and self-encompassing figure, this is recommended further reading. Now I’ll focus on further interesting links between Klee, Escher and Duchamp with respect to the use they made of the well-known topological properties of those surfaces. The analogy between the infinity-shaped motif of Klees’ and Eschers’ Moebius strips is further reinforced by observing some other prints of Escher’s, which came 10 or 15 years before his Moebius strips; Horsemen (1946) (Fig. 20) and Predestination (1951) (Fig. 21) show the planar infinity-shaped motif. Let us take Duchamp’s
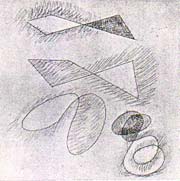
Steeplechase (Fig. 22): it is a
self-made racing course, for a childish horserace game in which there
is a clear connection with both Klee’s infinity-shaped motif and Escher’s
prints Horseman and Predestination. This could be seen
as an antecedent of Sculpture for Travelling (1918). (Fig.
23) >>Next
Notes
Figs.
22-23
|
|||||||||||||||||||||||||||||||||||||