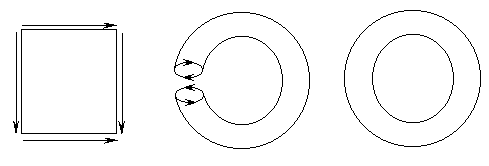
| And now the last step. Referring once again to the rectangle in the 2D space, let's maintain the two rules for the entrance and the exit of the horizontal and vertical edges of the figure, and let's introduce a minute but important alteration in the second one: when we go out from the top side we could re-enter from the bottom swapping left and right, and vice versa (Fig. 36B and 36C).
It is easy to
show that when we pass from the cylinder to the torus we haven't such
a swapping between left and right. See in Fig. 35A
the edges of torus before the closing: we go along the two circles walking
with the same orientation (clockwise or anticlockwise in both the cases).
So, the torus doesn't
agree with the new swapping of the second rule. We only obtain the desired
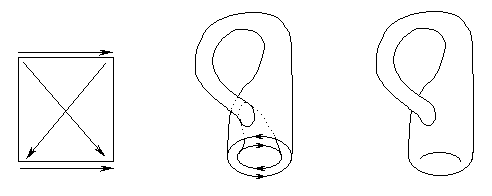
effect if the starting cylinder penetrates itself (with a self-intersection)
before closing itself, as depicted in Fig.
36A
The new strange figure is called Klein Bottle (from the mathematician Klein). The Animation A1 helps us visualize the formation of the bottle starting from a simple rectangle, by means of two simultaneous circular closings. (En passant: we must admit that a kleinian surface would be a very good place to draw a suicide saw!) This object has many strange topological properties, among which we cite the most important for the present context: while the torus has two faces (internal and external) the Klein bottle has only one face, because with this figure we lose the distinction between inner and outer, as we can easily verify with a little effort of imagination, in a mental exploration of the object. Animation A2 may serve to illustrate this aim. All this agrees with the note's statement: "The interior and the exterior (in a fourth dimension) can receive a similar identification." An interesting question arises: does Duchamp's hint to the 4D space in this note have a correspondence with the well known fact that in a 4D space, we could realize a kleinian bottle without intersecting surfaces? Rosen presents the necessity of a fourth dimension for the building of a kleinian bottle without self-penetration clearly and intuitively in a non-technical manner with some important philosophical implication (1997). Finally, we can hypothesize a possible meaning for the enigmatic final statement about the axis, that is no longer vertical and has no longer a one-dimensional appearance--if we look at the axes as the lines along which we close the rectangle twice (the first time for the passage to the cylinder and the second time for the passage to the Klein Bottle) we no longer have one axis but two, so we no longer have unidimensionality.
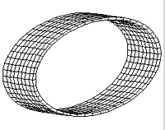
In the construction of a kleinian bottle I showed that in order to obtain the left-right swapping during the second conjunction, self-penetration is necessary. It is, however, possible to have a similar swapping by cutting a cylinder and re-closing the surface after a 180° torsion, as showed in Animation A3. It originates a topological figure called Moebius band; this strange figure has a single face and a single edge. From the conjunction of two Moebius bands along their sole edges, we obtain a kleinian bottle, as Animation A4 may help visualize.
In the realization of the Sculpture for Traveling (1918) (Fig. 37), Duchamp seems to use a technique, which quite nearly recalls some of the procedures previously described. It is well known that he glued to each other several irregular colored rubber strips, cut from bathing caps. The original object is lost, so we must refer to the historical photo and to the description that Duchamp himself did. With some difficulties, some self-penetration and some torsion can be possibly discerned in the historical photos; the description of the work made by Duchamp to Jean Crotti (Effemeridi, July 8th, 1918) talks about rubber strips "glued together, but not flat" (italics mine). I think he alluded to some torsion (as the one necessary for the Moebius band) before the gluing. From the same source we learn that Duchamp considered the Traveler's Sculpture more interesting than the painting Tu m'. >>Next Fig.
37
page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |