Now, if Duchamp really let the threads drop down, then there must be some device to hold the distance between the extremities during the drop in such a way that they remain constant. At this point, we can conjecture several different techniques of execution, consistent with three types of evidence:  what we can see in the Stoppages, what is described in the Green Box note, and what Duchamp claimed in several interviews. A few possible examples follow.

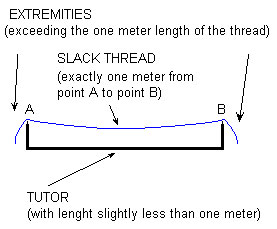
The first hypothetical device may be a simple tutor, as in the sketch in Fig. 4 (below)-- the tutor would drop together with the thread.        

Fig4

Stoppages Device 1

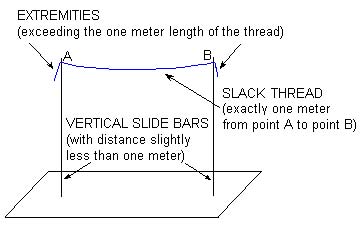
The surplus of thread relative to the regular length of one meter, visible at the extremities of the device, would make up the stretches necessary for the tacking that we observe on the back side of the canvases. (They could already have the needle necessary for the tacking inserted.)

Two vertical slide bars could form another device, depicted in Fig. 5 (below). Like the first example, in this case, we could have a thread surplus for the tacking at the opposite extremities of the thread.

Fig5

Stoppages Device 2

Although we must look at these devices as pure conjecture, we can at least acknowledge that in both cases, during the drop they would permit the thread to twist as it pleases, to keep that smooth linearity that seems impossible to obtain by dropping the thread freely, and to hold the distance between the extremities constant. Furthermore, (save for some mischievous reticence) the procedure described in the Green Box would turn out truthful and disprove notions that Duchamp was dishonest during the interviews.

However it turns out, by looking at Three Standard Stoppages we can consider two fixed points A and B, and three lines running through them, as showed in (Fig. 6).

This can evoke in our mind the Euclidean axiom of existence and unicity of the straight line through two points. It is well known that the Stoppages' motif often reappears in Duchamp's other works and acts as a basis for the development of further important conceptual ideas. We can consider that it is not arbitrary to think of this work as a sort of axiom, starting from which Duchamp deduces the construction of the whole building of his work (not exclusively geometric). However, it is important to realize just what exactly this axiom exerts.

In his funny and seemingly naive manner, it appears that Duchamp wants to remove from the Euclidean axiom the assumption of the unicity of the straight line through two points: the straight lines would be infinite, all of them obtained randomly by dropping the thread, and the three Stoppages representative of all of them (after all, we must remember that often in Duchamp’s work, “3” stands for multiplicity or infinity.) Indeed, we have known for quite some time that Duchamp was very interested in non-Euclidean geometry. Henderson states that:

page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15