|
Drawing the Maxim from the Minim: The Unrecognized Source of Niceron's Influence Upon Duchamp by Stephen Jay Gould and Rhonda Roland Shearer |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
When a skilled trickster poses a problem that either cannot be solved for logical reasons, or cannot be answered without information purposely destroyed beyond all possibility of recovery, then we rightly brand our adversary as cruel, perverse, or (at the very least) unfair. But when a master trickster hides a solution by a simple device that demands some unadvertised effort from our end, then we appreciate the depth and challenge all the more for demanding our input without deigning to inform us in any explicit manner. Duchamp, in purveying his wares at the pinnacle of this second, and wondrously engaging, strategy, made nothing easy for us, if only because he invariably hid his most profound insights, and his most important sources, in "trivial" jottings and scribblings, or in off-the-cuff pronouncements of no apparent significance.
The White Box
notes include a stunning example of this genre of ultimately fruitful
misleading in a scribble that honors, for a particularly mordant and
interesting reason, the wrong object in the right category. And, so
far, everyone has fallen for the literality of Duchamp's note. The nub
of the problem may be briefly stated in both its general
and specific form: Duchamp insisted, over and over again and in no uncertain
terms, that he had read all the great treatises in classical perspective,
and that he remained committed to its ideals and insights. He also stated,
in a forceful claim well known (and much discussed) by Duchamp aficionados,
that he wished to "rehabilitate" classical perspective, and
that he had obeyed its precepts in constructing his masterpiece, the
Large Glass. More specifically, he claimed that, as a young man,
while working at the great research library of Sainte Geneviève (1913-14),
he had read their entire section of antiquarian books on perspective.
But he only mentioned one author and one work by name, in a White
Box note much pored over by scholars :
This note refers to the 1646 Latin treatise on optics, the Thaumaturgus opticus of the French mathematician, Father Jean-François Niceron of the Order of Minims. Several scholars have studied this book for indications of specific influences upon Duchamp in general and, in particular, for any clue about Duchamp's choice of this volume and author, among all others, for explicit citation and praise. So far, they have failed. Thaumaturgus is a fine work, and Niceron was a fine scholar. The volume does present a good summary of optics and perspective based on direct vision. But nothing in this work seems particularly Duchampian, or particularly distinctive within this important genre of 17th century scholarship. (Niceron maintained a special interest in anamorphosis, as did Duchamp. But several other mathematicians and physicists of the time had written with equal verve and depth on this subject).
As for the larger mystery, scholars have simply and uncritically accepted Duchamp's claim that he rigorously used these principles in his major works. Ironically, however, no one who actually attempted the experiment has ever been able to render the bachelor machinery of the Large Glass under classical perspective, unless they alter Duchamp's own drawings and therefore conclude that he was not, after all, a very accurate geometer. The Chocolate Grinder, especially, does not seem properly drawn, and no one has been able to show how the device might turn without the wheels interpenetrating and thus, to make the metaphor literal, grinding to a halt. Other famous items in Duchamp's work - including the Given torso and the odd bends and angles of the hooks in the sole depiction of Trébuchet - seem similarly disobedient to his stated claims about using or rehabilitating classical perspective. We cannot solve this larger mystery here, but we can at least demonstrate that a proper reading of the Niceron note, and a deciphering of Duchamp's drollery in making this influence difficult for us to discern, can identify the important and quite specific influences of Niceron upon Duchamp, and may also point towards a general resolution of Duchamp's hidden theory of truly rehabilitated perspective - with proper homage to the Renaissance and Baroque masters carried forward to rigorous Duchampian novelty. Jean-François Niceron (1613-1646) joined the Order of Minims and studied under their greatest scholar, the mathematician Marin Mersenne (1588-1648). In 1639, he became professor of mathematics at the order's convent in Rome, Trinita dei Monti (where anamorphic works and other trompe l'oeil paintings of this age may still be seen on the curved vaults of the chapel). But, in 1640, his superiors also assigned him as official visitor to the order's other monasteries. These frequent travels weakened Niceron's perennially frail health (a condition probably not aided by the austere life style of the Minims, including a strictly vegan diet), and he died, at age 33, while visiting the monastery of Aix in 1646. Moving to the main biographical point of Niceron's work and Duchamp's note, Niceron had intended to publish a fully serious and technical Latin monograph on all aspects of his studies in geometric optics. His full treatment would have included four books, the first an introduction based upon methods for drawing the five regular solids on two dimensional surfaces, especially on the curves and arcs so commonly encountered on church ceilings; the second on "optics, or direct vision"; the third on "catoptrics, or viewing by reflections in flat, cylindrical and conical mirrors"; and the fourth on "dioptrics, or viewing by refraction through lenses." But Niceron died with the manuscript unfinished, and the text of Thaumaturgus opticus, edited by his friend and mentor Mersenne, only included the material of the first two books, leaving Niceron's work on mirrors and refractions unpublished in his Latin culmination. In fact, Thaumaturgus opticus includes the poignant statement from Niceron that he will treat mirror reflections and lens refractions in a future volume "si Deus faverit, otiumque et vires ex eius immensa bonitate suppenditent" (if God will grant me, by his immense goodness, the leisure and the strength).
We know the intended content of Niceron's plans for his uncompleted Thaumaturgus because this partial Latin swansong is a vastly expanded, "cleaned-up," and conventionally scholarly version of a much shorter, charming and delightful, playful and quirky, but mathematically exact and rigorous French treatise that he had published in 1638 as "La perspective curieuse, ou magie artificielle des effets merveilleux" (Curious perspective, or artificial magic of marvelous effects). Duchamp's style and personality simply did not tune well with the Latin technicality of Thaumaturgus, but I cannot imagine a better match of interest and temperament, or a better confluence of pure personal sympathy, than the Niceron of La perspective curieuse and Duchamp in the years just before World War I, as he painted his Nude descending; wrote the notes that would appear so much later in the Green and White boxes; studied perspective, dimensionality, optics and science; and set his life's work and course.
The two men even looked a bit alike, as the frontispiece of Niceron from Thaumaturgus opticus indicates. When he published La perspective curieuse, Niceron was 25 years old - the same age as Duchamp when he displayed Nude descending at the Armory Show of 1913. More importantly, the chatty and irreverent tone of Niceron's La perspective curieuse - so diametrically different from the highly formal Latinity of Thaumaturgus - surely had enormous appeal for Duchamp, who must have found, in Niceron's vernacular work, a kindred spirit from a baroque world 300 years past. To cite just one theme that delighted both men, Niceron loved puns and anagrams, and festooned La perspective curieuse with such amusing asides - though not a single one breaks through into Thaumaturgus opticus. For example, speaking of mirrors and their powers of reversal, Niceron presented an experiment involving King Francis I (see forthcoming discussion), but then digresses to state that when the current King Louis visited Bordeaux in 1615, the local citizens placed an anagrammatic banner under their triumphal arch: "Lois de Bourbon, bon Bourdelois" - or, Louis of Bourbon (the family name of the French Kings), good man of Bordeaux. Duchamp would later construct several anagrams of exactly the same nature, where two sequences use the same syllables (and spelling), but in different order and with disparate meanings. King Louis's anagram is perfectly palindromic by syllables, whereas the following contribution by Duchamp runs the last four syllables of the second line as 4,2,3, and 1 in contrast with 1,2,3,4 of the first line, thus yielding the salacious:
Niceron then embellishes his best example in dioptrics - his "conversion" of the faces of 12 Turks to the head of King Louis XIII (to be discussed later as a potentially important influence upon Duchamp's greatest innovation in perspective) - with a lovely Latin anagram devised by a friend, and stating Niceron's achievement with an anagram of his own name:
At least three scholars well versed in the science of Duchamp's interests in optics and perspective (Jean Clair, Linda Henderson and Craig Adcock) have followed Duchamp's literal instruction, and searched Thaumaturgus opticus to locate the influence of classical works upon Duchamp's understanding of perspective. But they found nothing beyond the undoubted status of Thaumaturgus as a good and standard text for its time. But when did Duchamp ever tell us anything directly, without placing us on some primrose path in the wrong direction, reversible only by our willingness to assume the role that Duchamp assigned to all students of the arts - the move from passive spectator to active interrogator by the recruitment of underutilized gray matter to transcend the merely retinal? In this particular case, we suspect that Duchamp's note purposely cited the wrong work of the right person - a "wicked" little experiment to see if anyone, failing to find any resolution of his claim in Thaumaturgus, would bother to consult Niceron's other work. Indeed, we do know that La perspective curieuse also graces the shelves of the Ste. Geneviève library, if only because Henderson (1983, p.144) found the book there, noted its explicit discussion of catoptrics and dioptrics, acknowledged that "there are differences between the two books," but erred in assuming a broader range in Thaumaturgus (perhaps from its far greater length), and then failed to recognize that two tantalizing potential sources for specifically Duchampian themes lie in the very sections of La perspective curieuse - the catoptrics of mirrors and the dioptrics of lenses - that receive no treatment at all in Thaumaturgus because Niceron died before reaching parts 3 and 4 in the projected Latin culmination of his life's work. We will close this article by discussing and figuring these two lovely and quite specific examples from Niceron, but we also wish to note in passing that the sections on catoptrics and dioptrics in La perspective curieuse (that is, the missing books of Thaumaturgus opticus) include several other shorter hints and passages that would repay further study, and that probably indicate an even greater influence of Niceron upon Duchamp. Consider just three short examples: 1. An extensive and learned literature has treated the optics in Duchamp's wonderfully rich construction entitled "A regarder (l'autre côté du verre) d'un oeil, de près, pendant presque une heure" - a work whose effect arises, at least in part, from its incorporation of a lens that is flat on one side and strongly convex on the other, yielding (when viewed from both sides and at different distances) both enlargements and diminutions, and both recto and inverted images. In book 3 on catoptrics in La perspective curieuse, Niceron describes these very properties of just such a lens (p.76):
2. The division of one into many, and the gathering together of many into one, stand as powerful and pervasive themes throughout Duchamp's oeuvre, not only (of course) for their visual effects, but primarily for their conceptual meanings and metaphors about our construction of reality, and of the various dimensions of perception and understanding. The point, needless to say, is scarcely original with Niceron, and has been known and employed both for light humor and dark magic ever since the invention of decent mirrors. But Niceron writes with special charm, and at interesting length, about the power of mirrors to multiply and conjoin, at least to our retinas (and to the delight or consternation of our gray matter) - as in this passage on page 77:
3. Galileo, Pope Urban VIII, and some common misconceptions about the false "warfare" between science and religion. Although not specific to any particularly Duchampian concern, we wish to indicate, in paying homage to the unfairly neglected Niceron, just one example of general insights about the history of art and science that such great works by generous intellects can supply. Niceron was a loyal Catholic priest and a fine scientist. He retained unquestioned fealty to the incumbent Pope Urban VIII who, in 1633, had enjoined Galileo's appearance before the Roman Inquisition; forced his public recantation of the correct heliocentric, or Copernican, theory of the solar system; and then placed him under the equivalent of house arrest for the remainder of his life. (Galileo died in 1642, four years after the publication of La perspective curieuse). Niceron, as a good scientist, revered Galileo, understood the legitimacy of his arguments for a central sun and a revolving earth, and particularly respected Galileo's pioneering telescopic observations of the heavens. In fact, Mersenne first learned of Galileo's death in a letter sent to him from Rome by Niceron, with its moving statement that "mathematicians must now mourn because their glory has been extinguished with the death of Galileo." Because the Church condemned Galileo, and because the Pope held such unquestioned authority, scholars have often assumed that (at least in Catholic circles), heliocentrism could not be mentioned, while Galileo himself became "unpersonned," placed even beyond the pale of explicit citation. In fact, although we propose no massive revisionism (and Galileo must remain the hero and martyr, with Urban the villain, of this particular tale), the actual story embodies far greater richness and complexity. The Church held a generally positive attitude towards science, and their astronomers knew the power of Galileo's argument. Galileo's books remained on the Index, and his "official" rehabilitation only occurred at the end of the last century. But heliocentrism prevailed within a generation or two, and although Catholic scientists needed to remain diplomatically circumspect in their published statements, Galileo's work and discoveries prevailed. Niceron's La perspective curieuse gives us direct insight into these interesting complexities. He praised (and depicted as we shall soon see) Urban VIII as the present Vicar of Christ on Earth, and as both the spiritual and temporal prince of Niceron's own conceptual world and actual real estate. But Niceron also mentioned and praised Galileo in La perspective curieuse (although not, needless to say, for his heliocentrism, but rather for his telescopic observations). In a key passage of the introduction to Book IV on dioptrics (refraction through lenses), Niceron states that, although the invention of the microscope and telescope (both, in usable form, by Galileo, by the way) had marked the greatest triumph of dioptrics, Niceron would focus on more playful and less practical utilities that should also be deemed worthy of interest. He then mentions Galileo, first and explicitly, in a list of scientists who "thanks to God and this great invention" (p.101) have revealed "new planets around Jupiter. . . and have recognized that Venus, as well as the moon, has phases that I have seen several times myself in broad daylight by means of these wonderful new glasses (lunettes)." We now close this treatment of Niceron and Duchamp with longer discussions (and depictions) of the two phenomena - one from book three on catoptrics, and one from book four on dioptrics, the two subjects not treated in Thaumaturgus opticus - that may well have provided crucial sources (or at least tweaking and initiating suggestions) for two of Duchamp's most important themes, both previously overlooked in Niceron because scholars relied on Duchamp's mislead and read only Thaumaturgus opticus, and not La perspective curieuse, with its deep and incisive discussions of these two curiosities, later promoted by Duchamp to centerpieces of insight about human vision and conceptualization:
1. The Wilson-Lincoln Effect. Ever since we began to study Duchamp, we have been amused by a wonderful little trick of human manipulability that he scarcely invented, but that he used with consummate skill and chutzpah: no matter how absurd it may be, if you say it often enough, and definitely enough - and especially if you say it with the subtle implication that everyone who's anyone knows it to be true - then your pure confabulation can quickly become an established verity. We do not, of course, claim that Duchamp, or Niceron for that matter, first developed the system of folded prisms that Duchamp called the "Wilson-Lincoln Effect" - that is (see the animated figure) the cutting up and placement of strips of two distinct images on separated but parallel planes of prisms, so that one discrete and reaggregated picture emerges from one point of sight, and the other from a different point of sight at right angles to the first. But we are pretty darned sure that no one ever thought of using Presidents Lincoln and Wilson as the two exemplars, and we definitely know that the phenomenon never bore such a patently absurd designation before Duchamp's "wicked" christening. After all, Lincoln was the first Republican president, and Wilson theDemocratic incumbent when Duchamp first moved to America, and the only Democrat besides Grover Cleveland who had managed to occupy the White House between Lincoln and World War I. (Perhaps Duchamp decided to invent the conjunction because Wilson was the man then holding the job, and Lincoln the most famous of his predecessors. In any case, we have searched on the Internet and eBay, questioned hobbyists, collectors of memorabilia, political buffs and historians. No one can find a single object of any sort, not to mention a set of prisms, featuring Wilson and Lincoln in any kind of exclusive conjunction - and the very concept makes most professional historians and collectors of political memorabilia laugh). But virtually any art historian will speak of the "Wilson-Lincoln effect" as a well known term for a phenomenon of optics - equivalent, we suppose, to such "urban legends" as the uncontested "fact" that we use only 10 percent of our brains (some folks will vociferously insist that they've heard 15 or 20 percent, even though the entire concept and formulation can only be labeled as ridiculous); or the undisputed street certainty of the senior author's childhood in Queens (yeah, we really did discuss such things on the sidewalks of New York) that only three people in the entire world understood Einstein's General Theory of Relativity. In any case, whatever the name, we can easily understand Duchamp's fascination with this system, especially given his particular interest in 90 degree rotations, both as a perceptual phenomenon and as a wonderful metaphor for completely independent points of view - a geometrically and mathematically accurate image by the way, because axes at right angles to each other ("orthogonal" in technical parlance) are mathematically independent, and thus define separate dimensions. (Mathematically speaking, for example, a four dimensional figure resides in a space defined by four mutually orthogonal axes - a concept that we cannot visualize in our three-dimensional world, but that can easily be expressed and manipulated in numerical terms).
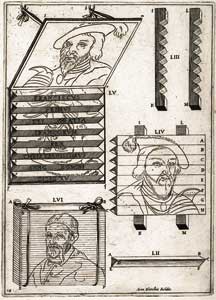
We do not know who first invented this system of two different icons orthogonally expressed on adjacent faces of triangular prisms (the "Wilson-Lincoln effect" of Duchamp's sly terminology). But we do know that Niceron illustrated a lovely example on Plate 18 of the third book (on catoptrics) of La perspective curieuse, accompanied by a fascinating discussion on pages 78-80 of the text. Niceron probably built the structure shown in this figure, for he was both an artist and tinkerer, and several of his optical machines, including some constructions far more complicated than this prismatic device, were seen and described by contemporary scientists, while two still survive in the Museo di Storia della Scienza (the museum for the history of science) in Florence. Pay no attention to Pope Urban VIII of Figure LVI, for he represents a different experiment. But Figures 52 to 55 illustrate Niceron's version of the Wilson-Lincoln system, featuring a great king (François Premier, or Francis the First, of France), who lived and reigned a full 350 years before Mr. Lincoln poetically described the beginning of our nation as "fourscore and seven years ago."
Figure 52 represents a single wooden prism of the set. You place a strip of one icon (Lincoln, if you will) on each face of the set of prisms represented by plane CDEF on Figure 52, with strips of the other icon (Wilson if you will) on the corresponding set of planes ABCD. Figure 53 then shows the two vertical wooden boards, with slots cut out to receive the prisms. Figure 54 depicts one way of slotting in the prisms to reveal only one of the icons because only one plane of each prism now faces the viewer directly, leaving the other two planes invisible behind. But if we slot the prisms in a different order, and look "from behind" (so to speak), with an edge of each prism directly pointing at us - so that we can see the two sets of adjacent faces, each now at 45 degrees to our direct line of sight - then the Wilson-Lincoln system comes into full view.
In Niceron's particular case of Figure 55, he places the icon of King Francis in strips on the upper faces of each prism, and then projects the entire image of the King upon a mirror, placed above the prisms and inclined at an angle of 45 degrees to the vertical - therefore depicting (in mirror reverse) the discrete and entire face of the King (hence Niceron's placement of this experiment in his book on catoptrics, or mirror reflections). In this example, Niceron then places words (rather than another image of a different king) on the corresponding set of prisms - reading (in Latin): "Francis the First, by the grace of God, most Christian King of France, in the year of our Lord 1515." Thus, instead of Wilson and Lincoln, Niceron gives us Francis I (projected onto a mirror above) and a text to praise the same man. But the entire system represents what Duchamp much later called, and used to such great interest and purpose, the "Wilson-Lincoln effect." Is this the Kingly face that launched a thousand slips (and anachronisms in naming), and that led Duchamp to cite the wrong book of Niceron in a little trick to honor the right man and to delay our discovery of the reasons therefore? 2. The Truly Rehabilitated Perspective System of Multiple Points of Sight. We must save the full story for another time and book, although Shearer reveals and discusses the general conclusion in her article on Duchamp's hatracks in this issue of Tout-Fait. But Shearer has discovered that Duchamp, in reality, even trumped what he slyly claimed. He did, indeed, use and understand classical perspective (at a time when most artists despised the subject as hopelessly constraining and superannuated). And he did exactly what he said in devising a "rehabilitated" perspective of mathematical form and precision for constructing the Large Glass. But, in his usual cryptic way, he neglected to tell us that he had rehabilitated classical perspective not by reviving the pure Brunelleschian form, but by moving beyond to a more complex system of his own invention, based on "multiple points of sight." That is, and in too brief a summary, Duchamp drew or photographed the object that he wished to depict from a large number of different spatial locations, or literal "points of sight." He then cut out a piece of the complete object from each separate point of sight, and fused them all together into a single image that "looked funny" if you thought that the final product was supposed to represent the entire figure as seen with a single eye from one Brunelleschian spot - as in classical perspective. But - and now we come to Duchamp's particular genius and to his chess game against the world - Duchamp took great pains to make sure that his fused icon didn't look quite "funny enough" to raise automatic suspicions in any intelligent observer who might encounter the claim that Duchamp had used the classical tools of Renaissance perspective. In fact, Duchamp must have figured out a way to choose just enough independent points of sight, separated just as widely as he dared, to fuse a single image that could still be rationalized by someone who might believe Duchamp's stated intentions, but then be inclined to give him a pass with a rationale of the following sort: "Oh well, Duchamp tried, but he's not really that great an artist, at least in a painterly sense. After all, that's why he gave up painting in the first place. So I guess the Chocolate Grinder and the Given Torso, and Trébuchet look a bit weird because poor old Duchamp has terrific ideas but just can't paint very well. Charming fellow, though, isn't he? And so very French, with that certain savoir faire and je ne sais quoi." We do not know for sure where Duchamp first got his idea for this truly revolutionary (although purposely hidden), and mathematically accurate, system of geometrically correct perspective under the radically novel scheme of multiple points of sight. As this question represents the key to Duchamp's single most original and important contribution to the history of art and conceptual representation (again, see Shearer's "hatrack" article in this issue of Tout-Fait for more details), the full answer will probably be quite complex, and has not, in any case, been fully resolved as yet. But we can say, at the very least, that Jean-François Niceron, in Book IV on Dioptrics (Refraction Through Lenses) of La perspective curieuse of 1638, developed a theoretical system - and built at least two complex, working optical devices to illustrate the resulting phenomenon - that presage, in a striking manner, the "multiple point of sight" perspective system later invented by Duchamp, who then used this system throughout his career as the hidden glue for his linkage between science and art, and as his homage to the mathematical discoveries and achievements of the great perspectivists of Renaissance and Baroque art.
Niceron devotes most of Book IV to a description of this system and to his optical machines for representing two stunning cases. In the first example on Plate 24, Niceron presents a drawing of the heads of 12 Turkish sultans and rulers, the principal Islamic enemies of Christian Europe at the time (and the subject of Niceron's anagram discussed previously). Note how Niceron outlines and inscribes, within the full space of the Turkish heads, a set of diamonds, parallelograms, and other more irregular figures in faintly dotted lines, using parts of each Turk to delineate the pieces that he will then amalgamate into his surprising new figure. The previous Plate 23 shows the picture of the 12 Turkish heads on a vertical screen. The optical refracting instrument of his own invention appears at the top of the Plate, above the Turkish screen, as a hollow cylinder with a multifaceted lens affixed into one end and labeled ABC. The viewing cylinder is then mounted at right angles to the vertical screen of Turks (RQ in the figure below). When the image on the screen of Turks projects into the cylinder and refracts through the lens, each facet of the lens "passes along" just one of the pieces outlined by the faintly dotted lines on each Turkish head of Plate 24. These partial images of each Turkish head then refract through the lens and get fused and reconstituted on the viewer's side as - lo and behold! - a single discrete and coherent image of the French King Louis XIII, the military scourge of the Turkish infidels! In one of his playful textual reveries, Niceron then puts his mind to other potential uses of these lenses. Continuing with his (and Duchamp's) favorite theme of complementarity in extracting many from one or of fusing one from many - as previously explored, and quoted in this article, in Book III on mirrors - Niceron ruminates about a similar scene he might construct based on Ezechiel's vision of the valley of dry bones. He could place the separated bones on his vertical screen, and then refract the appropriate parts through his lens "to make them live, so well united and adjusted together that they would form a single skeleton with all proportions and parts in the right measure." By contrast, Niceron then imagines that he could exploit the reverse procedure by placing a single picture of Medea upon his vertical screen and then using a scattering, rather than a converging, refractive lens to produce a gruesome picture of Medea's dismembered sons, after she has them murdered and torn apart following her discovery of Jason's (that is, their father's) infidelity to her.
Just to show that he had invented a general and workable system, and not just a cute trick for a princely party, Niceron then presents an optically similar, but conceptually very different, example as Plate 25. He now draws the heads of 14 Popes on his vertical screen, and designates pieces of each head with the same device of faintly dotted lines. A picture of Jesus occupies the center of the screen, but Niceron dares not dismember God himself - so no section of Jesus' image contributes to the new figure discretely fused from pieces of all the popes. Note, for example, how Niceron uses just the keys (the symbol for the entire office!) From the picture of St. Peter, the first Pope of all, in figure N on the upper right. Now, as with the Turks just before, Niceron projects the dismembered pieces of the Popes through a refracting lens at one end of his cylinder and - lo and behold yet again! - in the center of the refracted image, in the place formerly occupied by Jesus himself, we see (as reconstituted from bits and pieces of all the other Popes) none other than the head of the current Pope, the Vicar of Jesus on Earth, Urban VIII, also the prosecutor of Galileo. Who ever said that life lacked its moral complexities amidst its geometric and scientific wonders! So if 12 Turks can be dismembered, and then fused to reconstitute a French king by refraction of multiple points of sight through a lens; and if 14 Popes can undergo a similar discombobulation to rebuild the current occupant of St. Peter's See - well, then, couldn't the human mind operate like Niceron's lens and build the world by forming mental images from multiple vantage points that cannot all be represented fully and simultaneously in our three-dimensional world, but that the brain can remember and reconstitute in the mind's eye of a four dimensional world - for our mental imagery can integrate the geometry of nature, the memory of different literal points of sight, and the temporal extension of our explorations from several spatial positions that cannot be literally occupied all at once. And if the mind really works this way, then couldn't an artist create a better representation for both our concepts and percepts by rehabilitating the limited and constraining classical perspective of a single eye from one point of sight - and devising a new and mathematically accurate system of perspective based on multiple points of sight, thereby depicting our mental reality more directly than ever achieved before? But surely, we must not tell anybody what we have done - for the mind must discover for itself what the mind has actually been doing during all these years of human (and even earlier) evolutionary history. Quite a project, and quite a prospect! Could a frail Minim, who died so young in 1646, have caught a glimpse of this truly higher reality - and then expressed his infectious germ of an insight, as is the wont of blessed and fallible humanity, in a grand jest about Turkish infidels and suboptimal Popes?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||